LeetCode 236. Lowest Common Ancestor of a Binary Tree

Problem

LeetCode 236. Lowest Common Ancestor of a Binary Tree

1. 题目简述

给出一棵二叉树树，给出其两个节点p和q，找出p和q的高度最低公共ancestor节点，本身也是自己的祖先节点。例如：

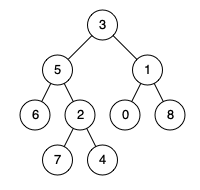
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.

2. 算法思路

recursion 或 stack + hash table

和二叉搜索树的问题不同，二叉树并没有其良好的有序性，不能取巧剪枝很多，所以要完全抛弃掉之前的思路。

那么如何进行查找呢？这里有两种思路。一种是递归，另一种是stack + hashmap。

第一种思路。对于某节点node，我们定义left，mid和right三个int变量，left变量表示在node的左节点上是否存在p或q节点(0不存在，1存在)，mid表示node节点本身是否存在p或q节点，right表示node的右子树上是否存在p或q节点。对于我们要找的目标节点target，left+mid+right一定是等于2的，而对于其他节点来说，left+mid+right最多为1，遍历整棵树，可得到目标节点。

第二种思路。我们先存储p的所有祖先节点，然后q节点不断向上找父节点，直到找到某个节点也在p的祖先节点列表中。我们用map来存储<node, father>键值对，进行遍历，直至map中的key包含了p和q。然后，将p一级级向上查找父节点，直至为null，存储到一个set中；随后对q进行同样操作，直至q包含在set中，此时，q记为所求。

注意，这里一层层遍历时，只能选择前序遍历或者BFS，不能选择中序遍历或者后续遍历，因为有”map.containsKey(p) && map.containsKey(q)”作为终止条件，后面两种遍历方式有可能导致ancestors的关系记录不完全！！！！有反例。

Corner Cases:
注意lowestAncestor是p或q本身的情况。

3. 解法

1. 递归

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    TreeNode lowestAncestor;

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        findPQ(root, p, q);
        return lowestAncestor;
    }

    private boolean findPQ(TreeNode node, TreeNode p, TreeNode q) {
        if (lowestAncestor != null) {
            return false; // 剪枝，更快一点点
        }
        if (node == null) {
            return false;
        }

        int left = findPQ(node.left, p, q) ? 1 : 0;
        int right = findPQ(node.right, p, q) ? 1 : 0;
        int mid = ((node == p) || (node == q)) ? 1 : 0;

        if  (left + mid + right == 2) {
            lowestAncestor = node;
        }

        if (left + mid + right > 0) {
            return true;
        }
        return false;
    }
}

2. 记录父节点

class Solution {
    TreeNode lowestAncestor;

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        Map<TreeNode, TreeNode> map = new HashMap();
        Set<TreeNode> ancestorP = new HashSet();
        Stack<TreeNode> stack = new Stack();

        map.put(root, null);
        stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            if (node.right != null) {
                stack.push(node.right);
                map.put(node.right, node);
            }
            if (node.left != null) {
                stack.push(node.left);
                map.put(node.left, node);
            }
            if (map.containsKey(p) && map.containsKey(q)) {
                break;
            }
        }

        while (p != null) {
            ancestorP.add(p);
            p = map.get(p);
        }

        while (q != null) {
            if (ancestorP.contains(q)){
                return q;
            }
            q = map.get(q);
        }

        return null;
    }
}