LeetCode 1457. Pseudo-Palindromic Paths in a Binary Tree

Problem

LeetCode 1457. Pseudo-Palindromic Paths in a Binary Tree

1. 题目简述

给你一棵二叉树，每个节点的值为 1 到 9 。我们称二叉树中的一条路径是 「伪回文」的，当它满足：路径经过的所有节点值的排列中，存在一个回文序列。

返回从根到叶子节点的所有路径中“伪回文”路径的数目。例如：

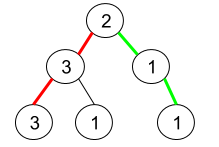
Input: root = [2,3,1,3,1,null,1]
Output: 2 
Explanation: 上图为给定的二叉树。总共有 3 条从根到叶子的路径：红色路径 [2,3,3] ，绿色路径 [2,1,1] 和路径 [2,3,1] 。

在这些路径中，只有红色和绿色的路径是伪回文路径，因为红色路径 [2,3,3] 存在回文排列 [3,2,3] ，绿色路径 [2,1,1] 存在回文排列 [1,2,1] 。

2. 算法思路

奇偶性

需要计算每条从root到根节点路径中每种数字的奇偶性，然后到达根节点时判断个数为奇数的数字是否最多只有一个。如果是，则res++；否则直接返回。

奇偶性 + bit manipulation

其实我们并不需要知道每种数字的具体个数，只要知道奇偶性即可。因此我们用一个10位bit来记录，如果为奇数，则bit位为1，偶数则bit位为0。最终判断bit位为1的个数。

3. 解法（LeetCode 105 & 106）

1. 奇偶性

使用Arrays.copyOfRange(int[] data, int start, int end)函数，写起来简洁，但是有点慢，而且耗空间大，因为要截取数组。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int res = 0;
    public int pseudoPalindromicPaths (TreeNode root) {
        int[] path = new int[10];

        Arrays.fill(path, 0);
        dfs(root, path);

        return res;
    }

    private void dfs(TreeNode root, int[] path) {
        if (root == null) {
            return;
        }

        path[root.val]++;

        if (root.left == null && root.right == null) {
            int countOdd = 0;
            for (int i = 1; i < 10; i++) {
                if (path[i] % 2 == 1) {
                    countOdd++;
                }
            }
            if (countOdd <= 1) {
                res++;
            }
        }

        dfs(root.left, path);
        dfs(root.right, path);

        path[root.val]--;
    }
}

2. 奇偶性 + bit manipulation，注意二进制里1个数的计算。另外，java不支持默认参数，所以需要另写一个辅助函数。

class Solution {
    public int pseudoPalindromicPaths (TreeNode root) {
        return getPseudo(root, 0);
    }

    private int getPseudo (TreeNode root, int s) {
        if (root == null) {
            return 0;
        }

        s ^= (1 << root.val);

        int ans = 0;
        if (root.left == null && root.right == null) {
            // 注意这里是怎么计算某数字二进制里1的个数的！
            int c = 0, x = s;
            while (x > 0) {
                x &= (x - 1); //每次去除最低位的1，直至全部为0
                c++;
            }
            ans += c <= 1 ? 1 : 0;
        }

        ans += getPseudo(root.left, s);
        ans += getPseudo(root.right, s);

        return ans;
    }
}