LeetCode 1035. Uncrossed Lines

Problem

LeetCode 1035. Uncrossed Lines

1. 题目简述

我们在两条独立的平行线线上按给定的顺序写下 A 和 B 数组。

我们可以绘制一些连接两个数字 A[i] 和 B[j] 的直线，只要 A[i] == B[j]，且我们绘制的直线不与任何其他连线（非水平线）相交。

以这种方法绘制线条，返回我们可以绘制的最大连线数。

Note:
1 <= A.length <= 500
1 <= B.length <= 500
1 <= A[i], B[i] <= 2000

Examples：

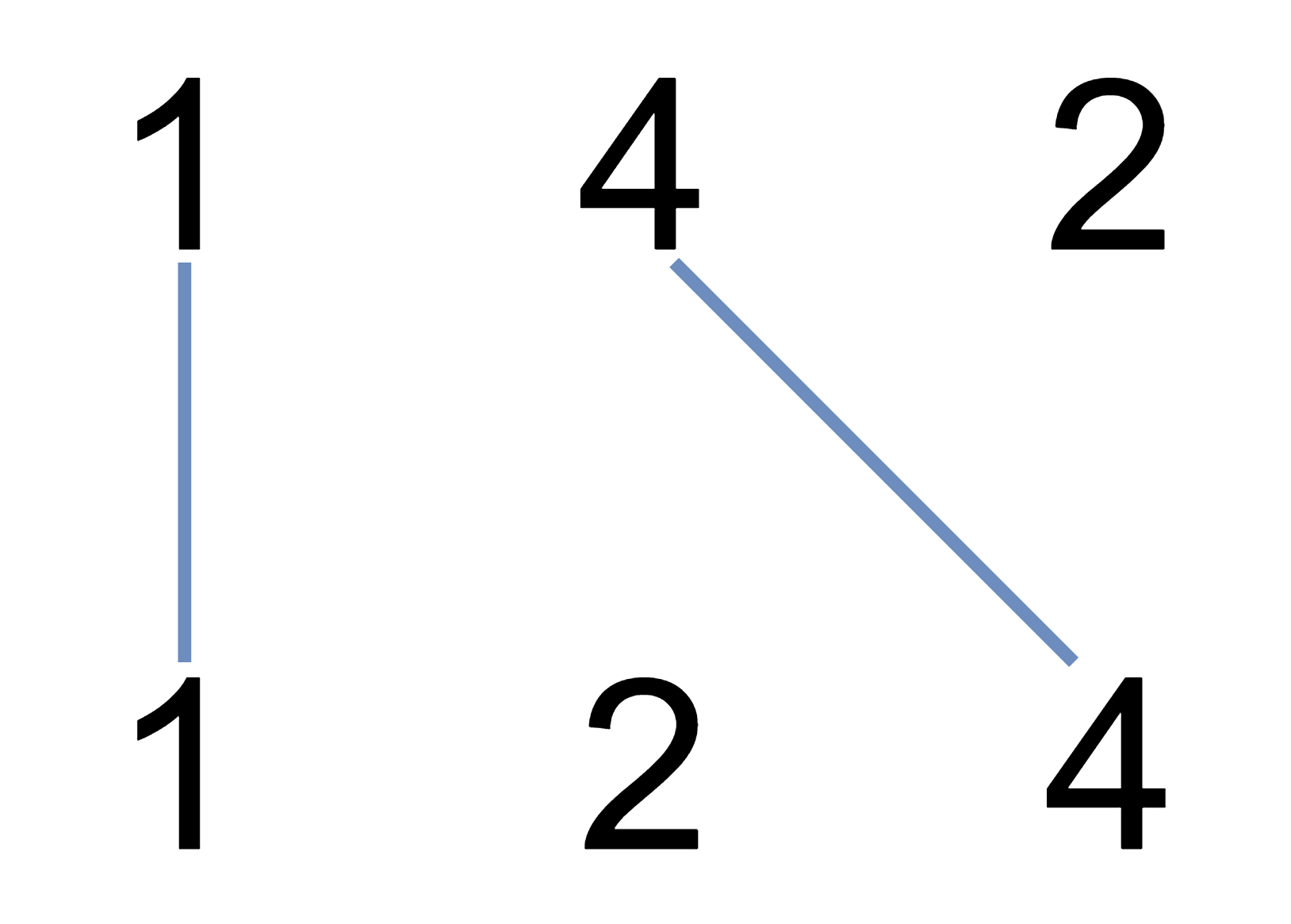
Input: A = [1,4,2], B = [1,2,4]
Output: 2
Explanation: We can draw 2 uncrossed lines as in the diagram.
We cannot draw 3 uncrossed lines, because the line from A[1]=4 to B[2]=4 will intersect the line from A[2]=2 to B[1]=2.

2. 算法思路

Dynamic Programming

又是二维数组，又是计算最大值，大概率是用DP来做。

我们假设**dp[i][j]**表示从A[0]到A[i]和B[0]到B[j]的子数组的最大连线数。

那么我们分为两种情况，第一种是A[i]和B[j]有连线，那么dp[i][j]就等于dp[i - 1][j - 1] + 1；如果没有连线，则dp[i][j]和max(dp[i - 1][j], dp[i][j - 1])相等，递推式如下：

\begin{equation}
dp[i][j] = dp[i - 1][j - 1] \text{ if } A[i] = B[j]
\end{equation}

\begin{equation}
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) \text{ if } A[i] \neq B[j]
\end{equation}

3. 解法

Dynamic Programming bottom-up：

class Solution {
    public int maxUncrossedLines(int[] A, int[] B) {
        int n1 = A.length, n2 = B.length;
        int[][] dp = new int[n1 + 1][n2 + 1];

        for (int[] row : dp) {
            Arrays.fill(row, 0);
        }

        for (int i = 1; i <= n1; i++) {
            for (int j = 1; j <= n2; j++) {
                if (A[i - 1] == B[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }

        return dp[n1][n2];
    }
}